Constituency methodology

Introduction

When policy changes in the UK - taxes, benefits, or public spending - it affects places and people differently. PolicyEngine UK builds tools to analyze incomes, jobs, and population patterns in each constituency. This documentation explains how we create a microsimulation model that works at the constituency level. The system combines workplace surveys of jobs and earnings, HMRC tax records, and population statistics. We map data between 2010 and 2024 constituency boundaries, estimate income distributions, and optimize geographic weights.

This guide shows how to use PolicyEngine UK for constituency analysis. We start with data collection, transform it for modeling, and build tools to examine policies. The guide provides examples and code to implement these methods. Users can measure changes in household budgets, track employment, and understand economic patterns on different constituencies. This document starts with data collection from workplace surveys, tax records, and population counts, then explains how we convert this data into usable forms through income brackets and boundary mapping. It concludes with technical details about accuracy measurement and calibration, plus example code for analysis and visualization.

Data

In this section, we describe three main data sources that form the foundation of our constituency-level analysis: earning and jobs data from NOMIS ASHE, income statistics from HMRC, and population age distributions from the House of Commons Library.

Earning and jobs data

Data is extracted from NOMIS Annual Survey of Hours and Earnings (ASHE) - workplace analysis dataset, containing number of jobs and earnings percentiles for all UK parliamentary constituencies from the NOMIS website. This dataset is stored as nomis_earning_jobs_data.xlsx. To download the data, follow the variable selection process shown in the image below:

Income data

Income data for UK parliamentary constituencies is obtained from HMRC. This dataset provides detailed information about income and tax by Parliamentary constituency with confidence intervals, and is stored as total_income.csv, including two key variables:

We use these measures to identify similar constituencies when employment distribution data is missing. Our approach assumes that constituencies with similar income patterns (measured by both taxpayer counts and total income) will have similar earnings distributions. The following table shows the dataset:

code name total_income_count total_income_amount
Loading ITables v2.2.4 from the init_notebook_mode cell... (need help?)

Population data by age

Population data by age groups for UK parliamentary constituencies can be downloaded from the House of Commons Library data dashboard. The dataset provides detailed age breakdowns for each UK constituency, containing population counts for every age from 0 to 90+ years old across all parliamentary constituencies in England, Wales, Northern Ireland, and Scotland. The data is stored as age.csv. The following table shows the dataset:

code name all 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90+
Loading ITables v2.2.4 from the init_notebook_mode cell... (need help?)

Preprocessing

In this section, we detail two key preprocessing steps necessary for our constituency-level analysis: converting earnings percentiles into practical income brackets, and mapping between different constituency boundary definitions (2010 to 2024).

Convert earning percentiles to brackets

To analyze earnings data effectively, we convert earning percentiles into earning brackets through the following process:

  1. First, we estimate the full distribution of earnings by:

    • Using known percentile data (10th to 90th) from the ASHE dataset

    • Extending this to estimate the 90th-99th percentiles using ratios derived from this government statistics report

  2. This estimation allows us to map earnings data into brackets that align with policy thresholds.

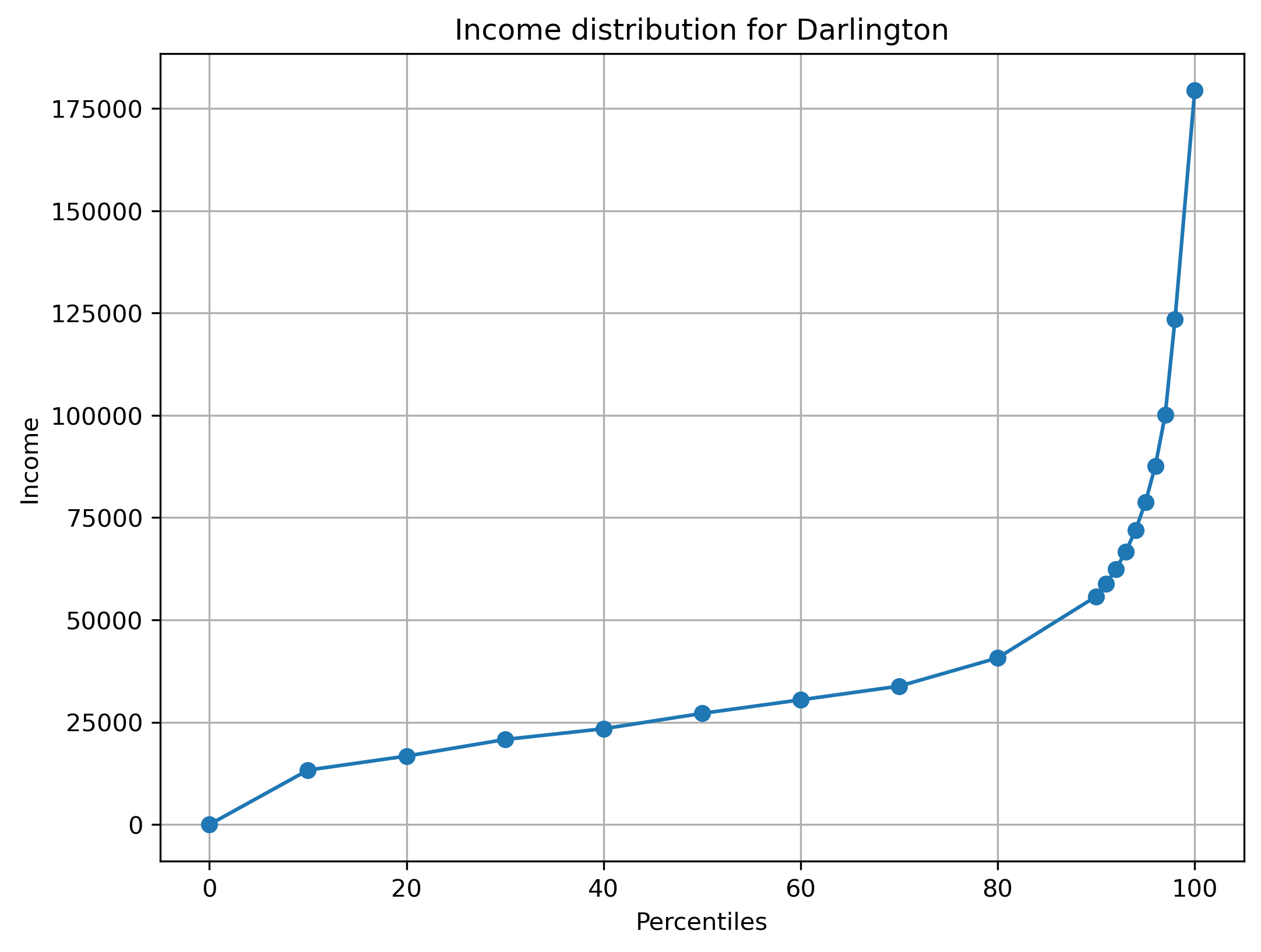
The following code and visualization demonstrate this process using an example constituency:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

# Sample data for Darlington
income_data = {
    'parliamentary constituency 2010': ['Darlington'],
    'constituency_code': ['E14000658'],
    'Number of jobs': ['31000'],
    '10 percentile': [13298.0],
    '20 percentile': [16723.0],
    '30 percentile': [20778.0],
    '40 percentile': [23407.0],
    '50 percentile': [27158.0],
    '60 percentile': [30471.0],
    '70 percentile': [33812.0],
    '80 percentile': [40717.0],
    '90 percentile': [55762.0],
    '91 percentile': [58878.0],
    '92 percentile': [62394.4],
    '93 percentile': [66722.3],
    '94 percentile': [71952.0],
    '95 percentile': [78804.5],
    '96 percentile': [87640.7],
    '97 percentile': [100083.5],
    '98 percentile': [123526.5],
    '100 percentile': [179429.0]
}

income_sample = pd.DataFrame(income_data)

# Excel Data Method
def load_real_data():
    # Read Excel data
    income_real = pd.read_excel("nomis_earning_jobs_data.xlsx", skiprows=7)
    income_real.columns = income_real.iloc[0]
    income_real = income_real.drop(index=0).reset_index(drop=True)
    
    # Select and rename columns
    columns_to_keep = [
        'parliamentary constituency 2010',
        'constituency_code',
        'Number of jobs',
        'Median',
        '10 percentile',
        '20 percentile',
        '30 percentile',
        '40 percentile',
        '60 percentile',
        '70 percentile',
        '80 percentile',
        '90 percentile'
    ]
    income_real = income_real[columns_to_keep]
    income_real = income_real.rename(columns={'Median': '50 percentile'})
    return income_real

# Plotting function
def plot_constituency_distribution(income_df, constituency_name, detailed=True):
    constituency_data = income_df[income_df['parliamentary constituency 2010'] == constituency_name].iloc[0]
    
    percentiles = [0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 91, 92, 93, 94, 95, 96, 97, 98, 100]
    income_values = [
        0,
        constituency_data['10 percentile'],
        constituency_data['20 percentile'],
        constituency_data['30 percentile'],
        constituency_data['40 percentile'],
        constituency_data['50 percentile'],
        constituency_data['60 percentile'],
        constituency_data['70 percentile'],
        constituency_data['80 percentile'],
        constituency_data['90 percentile'],
        constituency_data['91 percentile'],
        constituency_data['92 percentile'],
        constituency_data['93 percentile'],
        constituency_data['94 percentile'],
        constituency_data['95 percentile'],
        constituency_data['96 percentile'],
        constituency_data['97 percentile'],
        constituency_data['98 percentile'],
        constituency_data['100 percentile']
    ]
    
    valid_data = [(p, v) for p, v in zip(percentiles, income_values) if pd.notna(v)]
    filtered_percentiles, filtered_income = zip(*valid_data)
    
    plt.figure(figsize=(8, 6))
    plt.plot(filtered_percentiles, filtered_income, marker='o')
    plt.xlabel('Percentiles')
    plt.ylabel('Income')
    plt.title(f'Income Distribution for {constituency_name}')
    plt.grid(True)
    plt.show()

# Plot sample data (Darlington with detailed percentiles)
plot_constituency_distribution(income_sample, 'Darlington', detailed=True)

After estimating the full earnings distribution, we convert the data into income brackets. We calculate the number of jobs and total earnings for each constituency and income bracket based on the estimated earnings distribution. When we encounter constituencies with missing data, we estimate their earnings distribution pattern using data from constituencies with similar total number of taxpayers and total income levels.

The Python script create_employment_incomes.py generates employment_income.csv containing number of jobs (employment_income_count) and total earnings (employment_income_amount) for each constituency and income bracket. The following table shows employment and income across different brackets for constituencies:

code name employment_income_lower_bound employment_income_upper_bound employment_income_count employment_income_amount
Loading ITables v2.2.4 from the init_notebook_mode cell... (need help?)

Mapping constituencies from 2010 to 2024

PolicyEngine uses HMRC income data which aligns with 2010 constituency boundaries; to handle this issue and align it with 2024 constituency boundaries definitions, we follow these processes:

  1. Download the mapping data from the ONS website that contains the official lookup table between 2010 and 2024 Westminster Parliamentary Constituencies.

  2. Create a mapping matrix (650 x 650) which maps each constituency from 2010 to corresponding constituency in 2024 using the construct_mapping_matrix.py script. This is a many-to-many mapping, as 2010 constituencies can be split across multiple 2024 constituencies, and 2024 constituencies can contain parts of multiple 2010 constituencies. The matrix structure has rows representing 2010 constituencies and columns representing 2024 constituencies.

  3. For each row in the matrix (representing a 2010 constituency), normalize the weights so they sum to 1. This ensures that when we redistribute data from 2010 boundaries to 2024 boundaries, we maintain the correct proportions.

The following table represents this mapping matrix:

Unnamed: 0 E14001063 E14001064 E14001065 E14001066 E14001067 E14001294 E14001366 E14001599 E14001068 E14001140 E14001069 E14001570 E14001070 E14001352 E14001071 E14001360 E14001600 E14001072 E14001090 E14001073 E14001189 E14001074 E14001075 E14001076 E14001077 E14001078 E14001392 E14001403 E14001079 E14001375 E14001080 E14001196 E14001506 E14001081 E14001434 E14001082 E14001162 E14001083 E14001137 E14001084 E14001359 E14001384 E14001085 E14001421 E14001559 E14001285 E14001397 E14001086 E14001525 E14001087 E14001127 E14001088 E14001274 E14001330 E14001533 E14001089 E14001229 E14001414 E14001091 E14001092 E14001096 E14001097 E14001093 E14001094 E14001099 E14001100 E14001095 E14001098 E14001101 E14001382 E14001102 E14001450 E14001103 E14001145 E14001459 E14001104 E14001105 E14001106 E14001244 E14001567 E14001107 E14001183 E14001108 E14001166 E14001109 E14001391 E14001110 E14001111 E14001112 E14001329 E14001113 E14001114 E14001343 E14001288 E14001364 E14001115 E14001116 E14001363 E14001429 N05000012 N05000006 N05000007 N05000010 N05000008 N05000018 N05000009 N05000015 N05000011 N05000017 N05000016 S14000060 S14000061 S14000063 S14000070 S14000065 S14000066 S14000067 S14000107 S14000062 S14000091 S14000108 S14000069 S14000109 S14000072 S14000097 S14000073 S14000074 S14000075 S14000071 S14000076 S14000086 S14000077 S14000092 S14000104 S14000078 S14000096 S14000021 S14000080 S14000079 S14000082 S14000081 S14000027 S14000064 S14000083 S14000084 S14000085 S14000087 S14000088 S14000089 S14000106 S14000101 S14000090 S14000100 S14000093 S14000094 S14000098 S14000110 S14000099 S14000068 S14000095 S14000045 S14000048 S14000103 S14000105 S14000051 S14000102 S14000111 W07000112 W07000082 W07000094 W07000111 W07000098 W07000097 W07000103 W07000108 W07000081 W07000089 W07000091 W07000090 W07000107 W07000109 W07000101 W07000104 W07000105 W07000083 W07000096 W07000095 W07000102 W07000093 W07000100 W07000087 W07000085 W07000099 W07000106 W07000084 W07000086 W07000092 W07000088 W07000110
Loading ITables v2.2.4 from the init_notebook_mode cell... (need help?)

Methodology

This section describes our approach to creating accurate constituency-level estimates through three key components: a loss function for evaluating accuracy, a calibration process for optimizing weights, and the mathematical framework behind the optimization. To see how well this methodology performs in practice, you can check our detailed validation results page comparing our estimates against actual data at both constituency and national levels.

Loss function

The file loss.py defines a function create_constituency_target_matrix that creates target matrices for comparing simulated data against actual constituency-level data. The following process outlines how the function processes:

  1. Takes three main input parameters: dataset (defaults to enhanced_frs_2022_23), time_period (defaults to 2025), and an optional reform parameter for policy changes.

  2. Reads three files containing real data: age.csv, total_income.csv, and employment_income.csv.

  3. Creates a PolicyEngine Microsimulation object using the specified dataset and reform parameters.

  4. Creates two main matrices: matrix for simulated values from PolicyEngine, and y for actual target values from both HMRC (income data) and ONS (age data).

  5. Calculates total income metrics at the national level, computing both total amounts and counts of people with income.

  6. Processes age distributions by creating 10-year age bands from 0 to 80, calculating how many people fall into each band.

  7. Processes both counts and amounts for different income bands between £12,570 and £70,000, excluding people under 16 for employment income.

  8. Maps individual-level results to household level throughout the sim.map_result() function.

  9. The function returns both the simulated matrix and the target matrix (matrix, y) which can be used for comparing the simulation results against actual data.

Calibration function

The file calibrate.py defines a main calibrate() function that performs weight calibration for constituency-level analysis.

  1. It imports necessary functions and matrices from other files including create_constituency_target_matrix, create_national_target_matrix from loss.py, and transform_2010_to_2024 for constituency boundary transformations.

  2. Sets up initial matrices using the create_constituency_target_matrix and create_national_target_matrix functions for both constituency and national level data.

  3. Creates a Microsimulation object using the enhanced_frs_2022_23 dataset.

  4. Initializes weights for 650 constituencies x 100180 households, starting with the log of household weights divided by constituency count.

  5. Converts all the matrices and weights into PyTorch tensors to enable optimization.

  6. Defines a loss function that calculates and combines both constituency-level and national-level mean squared errors into a single loss value.

  7. Uses Adam optimizer with a learning rate of 0.1 to minimize the loss over 512 epochs.

  8. Every 100 epochs during optimization, it updates the weights using the mapping matrix from 2010 to 2024 constituencies and saves the current weights to a weights.h5 file.

  9. Includes an update_weights() function that applies the constituency mapping matrix to transform the weights between different boundary definitions.

Optimization mathematics

In this part, we explain the mathematics behind the calibration process that we discussed above. The optimization uses a two-part loss function that balances constituency-level and national-level accuracy, combining both local and national targets into a single optimization problem. The mathematical formulation can be expressed as follows:

For the constituency-level component, we have:

  • A set of households (\(j\)) with known characteristics (\(metrics_j\)) like income, age, etc.

  • A set of constituencies (\(i\)) with known target values (\(y_c\)) from official statistics

  • Weights in log space (\(w_{ij}\)) that we need to optimize for each household in each constituency

Using these components, we calculate predicted constituency-level statistics. For each constituency metric (e.g. total income), the predicted value is:

\[ \text{pred}_c = \sum_j (\exp(w_{ij}) \times \text{metrics}_j) \]

where \(\text{metrics}_j\) represents the household-level characteristics for that specific metric (e.g. household income). We use exponential of weights to ensure they stay positive.

To measure how well our predictions match the real constituency data, we calculate the constituency mean squared error:

\[ \text{MSE}_c = \text{mean}((\text{pred}_c / (1 + y_c) - 1)^2) \]

where \(y_c\) are the actual target values from official statistics for each constituency. We use relative error (dividing by \(1 + y_c\)) to make errors comparable across different scales of metrics.

For the national component, we need to ensure our constituency-level adjustments don’t distort national-level statistics. We aggregate across all constituencies:

\[ \text{pred}_n = \sum_i (\sum_j \exp(w_{ij})) \times \text{metrics}_\text{national} \]

with corresponding mean squared error to measure deviation from national targets:

\[ \text{MSE}_n = \text{mean}((\text{pred}_n / (1 + y_n) - 1)^2) \]

The total loss combines both constituency and national errors:

\[ L = \text{MSE}_c + \text{MSE}_n \]

We initialize the weights using the original household weights from the survey data:

\[ w_{\text{initial}} = \ln(\text{household}_{weight}/650) \]

where 650 is the number of constituencies. These weights are then iteratively optimized using the Adam (Adaptive Moment Estimation) optimizer with a learning rate of 0.1. The optimization process runs for 512 epochs, with the weights being updated in each iteration:

\[ w_{t+1} = w_t - 0.1 \times \nabla L(w_t) \]

This formulation ensures that the optimized weights maintain both local consistency at the constituency level and global accuracy for national-level statistics. The Adam optimizer adaptively adjusts the weights to minimize both constituency-level and national-level errors simultaneously, providing efficient convergence through adaptive learning rates and momentum. The resulting optimized weights allow us to accurately reweight household survey data to match both constituency-level and national statistics to obtain accurate estimates of income distributions, demographics, and policy impacts for each parliamentary constituency while maintaining consistency with national totals.

Example

The following code demonstrates how to analyze and visualize median earnings across UK parliamentary constituencies using PolicyEngine:

# Import required libraries
from policyengine.utils.charts import *
from policyengine import Simulation

# Initialize simulation for visualization
sim = Simulation(
    country="uk",
    scope="macro",
    time_period="2025",
    options={
        "include_constituencies": True,  # Enable constituency-level analysis
    }
)

# Add fonts for visualization
add_fonts()

# Define function to calculate median earnings for adults
def adult_earnings_median(sim):
    # Filter for working age adults (18-65)
    adult = sim.calculate("age").between(18, 65)
    # Get employment income
    earnings = sim.calculate("employment_income")
    # Return median of positive earnings for adults
    return earnings[earnings > 0][adult].quantile(0.5)

# Create and display visualization of median earnings by constituency
sim.calculate(
    "macro/gov/local_areas/parliamentary_constituencies",
    metric=adult_earnings_median,
    chart=True
).update_layout(
    title="Median earnings of adults in parliamentary constituencies",
)

This code demonstrates how to:

  1. Load and process constituency-level data using PolicyEngine’s microsimulation capabilities

  2. Calculate real household income and population metrics

  3. Apply constituency weights to generate accurate geographic distributions

  4. Create constituency-level visualizations of median earnings

  5. Filter for working-age adults (18-65) and positive earnings

  6. Generate an interactive visualization showing median earnings across parliamentary constituencies

The figure below shows the simulated results, displaying median earnings data across UK parliamentary constituencies in a geographic representation. The color intensity indicates earnings levels, providing an intuitive visualization of how earnings vary across different regions of the UK.

/opt/hostedtoolcache/Python/3.12.8/x64/lib/python3.12/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm